Sequence is a particular order in which related things follow each other. Its fun and its very intuitive and so called logical. So lets start.
NOTE: Here we are not going to discuss what are different types of sequences are. We will see how we can achieve different sequences using Python.
Geometric Sequence
In a Geometric Sequence each term is found by multiplying the previous term by a constant.
2, 4, 8, 16, 32, 64, 128, 256, …
This sequence has a factor of 2 between each number. Each term (except the first term) is found by multiplying the previous term by 2.
def gterm(n, cons): x = 1 for i in range(1,n): x = x * cons print x
Arithmetic Sequences
In an Arithmetic Sequence the difference between one term and the next is a constant.
1, 4, 7, 10, 13, 16, 19, 22, 25, …
This sequence has a difference of 3 between each number.
Its Rule is xn = 3n-2
>>> print range(1, 26, 3) [1, 4, 7, 10, 13, 16, 19, 22, 25]
Triangular Numbers
The Triangular Number Sequence is generated from a pattern of dots which form a triangle.
1, 3, 6, 10, 15, 21, 28, 36, 45, …
By adding another row of dots and counting all the dots we can find the next number of the sequence:

But it is easier to use this Rule: xn = n(n+1)/2
def triangle_numbers(n): return [i*(i+1)/2 for i in xrange(n)] >>> triangle_numbers(10) [0, 1, 3, 6, 10, 15, 21, 28, 36, 45]
Square Numbers
The next number is made by squaring where it is in the pattern.
Rule is xn = n2
1, 4, 9, 16, 25, 36, 49, 64, 81, …
def square_numbers(n): return [i*i for i in xrange(1, 10)] >>> square_numbers(10) [1, 4, 9, 16, 25, 36, 49, 64, 81]
Cube Numbers
The next number is made by cubing where it is in the pattern.
Rule is xn = n3
1, 8, 27, 64, 125, 216, 343, 512, 729, …
def cube_numbers(n): return [i*i*i for i in xrange(1, 10)] >>> cube_numbers(10) [1, 8, 27, 64, 125, 216, 343, 512, 729]
Fibonacci Sequence
In this sequence the next number is found by adding the two numbers before it together.
Rule is xn = xn-1 + xn-2
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
def F(n): if n == 0: return 0 elif n == 1: return 1 else: return F(n-1)+F(n-2)
Palindrome
A palindrome is a word, phrase, number, or other sequence of symbols or elements that reads the same forward or reversed, with general allowances for adjustments to punctuation and word dividers. Famous examples include “Amor, Roma”, “A man, a plan, a canal: Panama”, “Race car”, “Taco cat” and “No ‘x’ in ‘Nixon'”.
>>> name = "Abhilash" >>> name[::-1] 'hsalihbA'
Anagram
An anagram is a type of word play, the result of rearranging the letters of a word or phrase to produce a new word or phrase, using all the original letters exactly once; for example Doctor Who can be rearranged into Torchwood.
def isAnagram(str1, str2): str1_list = list(str1) str1_list.sort() str2_list = list(str2) str2_list.sort() return (str1_list == str2_list)
Pangram
Pangram is a sentence using every letter of the alphabet at least once. The best known English pangram is:
“The quick brown fox jumps over the lazy dog.”
import string, sys
if sys.version_info[0] < 3:
input = raw_input
def ispangram(sentence, alphabet=string.ascii_lowercase):
alphaset = set(alphabet)
return alphaset <= set(sentence.lower())
print ( ispangram(input('Sentence: ')) )
Prime Numbers
A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, …
import math for num in range(3,101,2): if all(num%i!=0 for i in range(2,int(math.sqrt(num))+1)): print num
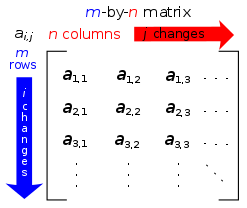
Matrix
In mathematics, a matrix (plural matrices) is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.
>&gt;&gt; import numpy as np >&gt;&gt; Y = np.array(list("ABCDE"*5)).reshape(5,5) >&gt;&gt; print Y [['A' 'B' 'C' 'D' 'E'] ['A' 'B' 'C' 'D' 'E'] ['A' 'B' 'C' 'D' 'E'] ['A' 'B' 'C' 'D' 'E'] ['A' 'B' 'C' 'D' 'E']] >&gt;&gt; print Y.transpose() [['A' 'A' 'A' 'A' 'A'] ['B' 'B' 'B' 'B' 'B'] ['C' 'C' 'C' 'C' 'C'] ['D' 'D' 'D' 'D' 'D'] ['E' 'E' 'E' 'E' 'E']] # Another way >&gt;&gt; matrix = [['A', 'B', 'C', 'D', 'E'], ['A', 'B', 'C', 'D', 'E'], ['A', 'B', 'C', 'D', 'E'], ['A', 'B', 'C', 'D', 'E'], ['A', 'B', 'C', 'D', 'E']] >&gt;&gt; print 'n'.join([' '.join(row) for row in matrix])
That’s fun, right. Keep checking I will post the Part – 2 as soon as possible. Also, give me your feedback on Twitter or post me a DM from here.
